在本教程中,我们将回答有关自动编码器的一些常见问题,并将介绍以下模型的代码示例
- 基于全连接层的简单自动编码器
- 稀疏自动编码器
- 深度全连接自动编码器
- 深度卷积自动编码器
- 图像去噪模型
- 序列到序列自动编码器
- 变分自动编码器
注意:所有代码示例均已于 2017 年 3 月 14 日更新至 Keras 2.0 API。您需要 Keras 2.0.0 或更高版本才能运行它们。
什么是自动编码器?
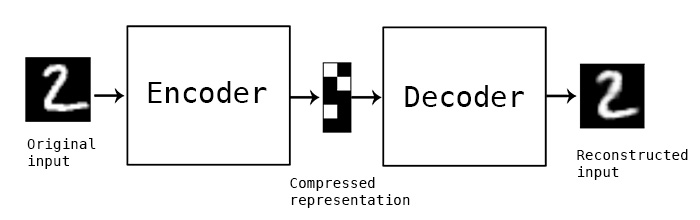
“自动编码”是一种数据压缩算法,其中压缩和解压缩函数是 1) 数据特定的,2) 有损的,以及 3) 从示例中自动学习,而不是由人类设计的。此外,在几乎所有使用“自动编码器”一词的情况下,压缩和解压缩函数都是使用神经网络实现的。
1) 自动编码器是数据特定的,这意味着它们只能压缩与其训练数据类似的数据。这与 MPEG-2 Audio Layer III (MP3) 压缩算法不同,后者只对一般的“声音”做出假设,而不是对特定类型的声音做出假设。在人脸图片上训练的自动编码器在压缩树木图片方面会做得很差,因为它学习到的特征是人脸特定的。
2) 自动编码器是有损的,这意味着解压缩后的输出与原始输入相比会有所降低(类似于 MP3 或 JPEG 压缩)。这与无损算术压缩不同。
3) 自动编码器是从数据示例中自动学习的,这是一个很有用的特性:这意味着很容易训练该算法的特定实例,使其在特定类型的输入上表现良好。它不需要任何新的工程设计,只需要适当的训练数据。
要构建一个自动编码器,您需要三样东西:一个编码函数、一个解码函数,以及一个衡量数据压缩表示与其解压缩表示之间信息损失程度的距离函数(即“损失”函数)。编码器和解码器将被选择为参数函数(通常是神经网络),并且相对于距离函数是可微分的,因此可以使用随机梯度下降法优化编码/解码函数的参数,以最小化重构损失。这很简单!您甚至不需要理解所有这些词就可以开始在实践中使用自动编码器。
它们擅长数据压缩吗?
通常情况下,不尽然。例如,在图像压缩中,训练一个比 JPEG 等基本算法做得更好的自动编码器是相当困难的,而且通常情况下,实现这一点的唯一方法是将自己限制在一种非常特定的图片类型(例如,JPEG 不擅长的图片)。自动编码器是数据特定的,这一事实使得它们通常不适用于现实世界的数据压缩问题:您只能将它们用于与其训练数据相似的数据,因此要使它们更通用,就需要大量的训练数据。但未来的进步可能会改变这一点,谁知道呢。
自动编码器有什么用?
它们很少用于实际应用中。2012 年,它们曾短暂地应用于深度卷积神经网络的贪婪逐层预训练 [1],但随着我们开始意识到更好的随机权重初始化方案足以从头开始训练深度网络,这种方法很快就过时了。2014 年,批标准化 [2] 开始允许使用更深的网络,从 2015 年末开始,我们可以使用残差学习 [3] 从头开始训练任意深的网络。
如今,自动编码器的两个有趣的实际应用是数据去噪(我们将在本文后面介绍)和用于数据可视化的降维。通过适当的维度和稀疏性约束,自动编码器可以学习比 PCA 或其他基本技术更有趣的数据投影。
特别是对于二维可视化,t-SNE(发音为“tee-snee”)可能是最好的算法,但它通常需要相对低维的数据。因此,可视化高维数据中相似性关系的一个好策略是,首先使用自动编码器将数据压缩到低维空间(例如 32 维),然后使用 t-SNE 将压缩后的数据映射到二维平面。请注意,Kyle McDonald 在 Keras 中开发了一个很好的 t-SNE 参数化实现,并在 Github 上提供。此外,scikit-learn 也提供了一个简单实用的实现。
那么,自动编码器有什么大不了的呢?
它们之所以出名,主要是因为它们出现在许多在线提供的机器学习入门课程中。因此,许多该领域的初学者都非常喜欢自动编码器,并且对它们爱不释手。这就是本教程存在的原因!
此外,它们之所以吸引了如此多的研究和关注,还有一个原因是,长期以来,人们一直认为它们是解决无监督学习问题(即在不需要标签的情况下学习有用表示)的潜在途径。然而,自动编码器并不是真正的无监督学习技术(这意味着完全不同的学习过程),它们是一种自监督技术,是监督学习的一种特例,其目标是从输入数据中生成的。为了让自监督模型学习到有趣的特征,你必须想出一个有趣的合成目标和损失函数,这就是问题所在:仅仅学习详细地重建输入可能不是正确选择。在这一点上,有大量的证据表明,例如,专注于像素级重建图像,不利于学习标签监督学习所诱导的那种有趣的抽象特征(其中目标是由人类“发明”的相当抽象的概念,如“狗”、“汽车”……)。事实上,有人可能会说,在这方面,最好的特征是那些在精确输入重建方面最差,但在您感兴趣的主要任务(分类、定位等)上却能取得高性能的特征。
在应用于视觉的自监督学习中,自动编码器式输入重建的一个潜在有效替代方法是使用玩具任务,如拼图游戏或细节-上下文匹配(能够将高分辨率但小的图像块与其提取的低分辨率图像版本相匹配)。以下论文研究了拼图游戏,读起来很有趣:Noroozi 和 Favaro (2016) 通过解决拼图游戏进行无监督视觉表示学习。这些任务为模型提供了传统自动编码器中缺少的关于输入数据的内置假设,例如“视觉宏观结构比像素级细节更重要”。

让我们构建最简单的自动编码器
我们将从简单开始,使用单个全连接神经层作为编码器和解码器
import keras
from keras import layers
# This is the size of our encoded representations
encoding_dim = 32 # 32 floats -> compression of factor 24.5, assuming the input is 784 floats
# This is our input image
input_img = keras.Input(shape=(784,))
# "encoded" is the encoded representation of the input
encoded = layers.Dense(encoding_dim, activation='relu')(input_img)
# "decoded" is the lossy reconstruction of the input
decoded = layers.Dense(784, activation='sigmoid')(encoded)
# This model maps an input to its reconstruction
autoencoder = keras.Model(input_img, decoded)
我们还要创建一个单独的编码器模型
# This model maps an input to its encoded representation
encoder = keras.Model(input_img, encoded)
以及解码器模型
# This is our encoded (32-dimensional) input
encoded_input = keras.Input(shape=(encoding_dim,))
# Retrieve the last layer of the autoencoder model
decoder_layer = autoencoder.layers[-1]
# Create the decoder model
decoder = keras.Model(encoded_input, decoder_layer(encoded_input))
现在让我们训练我们的自动编码器来重建 MNIST 数字。
首先,我们将配置我们的模型以使用每个像素的二进制交叉熵损失和 Adam 优化器
autoencoder.compile(optimizer='adam', loss='binary_crossentropy')
让我们准备我们的输入数据。我们使用的是 MNIST 数字,并且我们丢弃了标签(因为我们只对编码/解码输入图像感兴趣)。
from keras.datasets import mnist
import numpy as np
(x_train, _), (x_test, _) = mnist.load_data()
我们将所有值归一化到 0 到 1 之间,并将 28x28 的图像展平成大小为 784 的向量。
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))
print(x_train.shape)
print(x_test.shape)
现在让我们训练我们的自动编码器 50 个 epoch
autoencoder.fit(x_train, x_train,
epochs=50,
batch_size=256,
shuffle=True,
validation_data=(x_test, x_test))
经过 50 个 epoch 后,自动编码器似乎达到了大约 0.09 的稳定训练/验证损失值。我们可以尝试可视化重建的输入和编码的表示。我们将使用 Matplotlib。
# Encode and decode some digits
# Note that we take them from the *test* set
encoded_imgs = encoder.predict(x_test)
decoded_imgs = decoder.predict(encoded_imgs)
# Use Matplotlib (don't ask)
import matplotlib.pyplot as plt
n = 10 # How many digits we will display
plt.figure(figsize=(20, 4))
for i in range(n):
# Display original
ax = plt.subplot(2, n, i + 1)
plt.imshow(x_test[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# Display reconstruction
ax = plt.subplot(2, n, i + 1 + n)
plt.imshow(decoded_imgs[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()
这就是我们得到的结果。第一行是原始数字,第二行是重建的数字。使用这种基本方法,我们丢失了相当多的细节。

在编码表示上添加稀疏性约束
在前面的例子中,表示只受隐藏层大小(32)的约束。在这种情况下,通常发生的情况是隐藏层正在学习PCA(主成分分析)的近似值。但另一种限制表示紧凑性的方法是对隐藏表示的活动添加稀疏性约束,这样在给定时间内“激活”的单元就会减少。在 Keras 中,这可以通过向我们的 `Dense` 层添加 `activity_regularizer` 来实现
from keras import regularizers
encoding_dim = 32
input_img = keras.Input(shape=(784,))
# Add a Dense layer with a L1 activity regularizer
encoded = layers.Dense(encoding_dim, activation='relu',
activity_regularizer=regularizers.l1(10e-5))(input_img)
decoded = layers.Dense(784, activation='sigmoid')(encoded)
autoencoder = keras.Model(input_img, decoded)
让我们训练这个模型 100 个 epoch(添加正则化后,模型不太可能过拟合,可以训练更长时间)。该模型最终的训练损失为 0.11,测试损失为 0.10。两者之间的差异主要是由于在训练过程中将正则化项添加到损失中(约为 0.01)。
以下是我们新结果的可视化
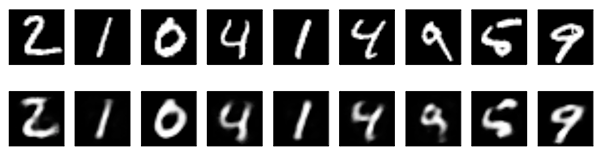
它们看起来与之前的模型非常相似,唯一的显著区别是编码表示的稀疏性。`encoded_imgs.mean()` 产生的值为 3.33(在我们的 10,000 个测试图像中),而之前的模型中相同的值为 7.30。因此,我们的新模型产生的编码表示稀疏度是之前的两倍。
深度自动编码器
我们不必将自己限制在单层作为编码器或解码器,我们可以使用多层堆叠,例如
input_img = keras.Input(shape=(784,))
encoded = layers.Dense(128, activation='relu')(input_img)
encoded = layers.Dense(64, activation='relu')(encoded)
encoded = layers.Dense(32, activation='relu')(encoded)
decoded = layers.Dense(64, activation='relu')(encoded)
decoded = layers.Dense(128, activation='relu')(decoded)
decoded = layers.Dense(784, activation='sigmoid')(decoded)
让我们试试这个
autoencoder = keras.Model(input_img, decoded)
autoencoder.compile(optimizer='adam', loss='binary_crossentropy')
autoencoder.fit(x_train, x_train,
epochs=100,
batch_size=256,
shuffle=True,
validation_data=(x_test, x_test))
经过 100 个 epoch 后,它达到了大约 0.08 的训练和验证损失,比我们之前的模型略好。我们重建的数字看起来也更好一些
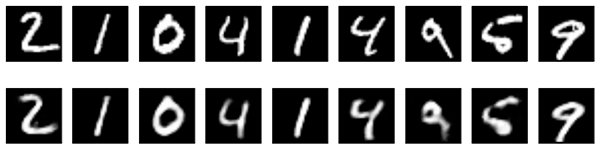
卷积自动编码器
由于我们的输入是图像,因此使用卷积神经网络 (convnet) 作为编码器和解码器是有意义的。在实际应用中,应用于图像的自动编码器始终是卷积自动编码器——它们的表现要好得多。
让我们实现一个。编码器将由一堆 `Conv2D` 和 `MaxPooling2D` 层组成(最大池化用于空间下采样),而解码器将由一堆 `Conv2D` 和 `UpSampling2D` 层组成。
import keras
from keras import layers
input_img = keras.Input(shape=(28, 28, 1))
x = layers.Conv2D(16, (3, 3), activation='relu', padding='same')(input_img)
x = layers.MaxPooling2D((2, 2), padding='same')(x)
x = layers.Conv2D(8, (3, 3), activation='relu', padding='same')(x)
x = layers.MaxPooling2D((2, 2), padding='same')(x)
x = layers.Conv2D(8, (3, 3), activation='relu', padding='same')(x)
encoded = layers.MaxPooling2D((2, 2), padding='same')(x)
# at this point the representation is (4, 4, 8) i.e. 128-dimensional
x = layers.Conv2D(8, (3, 3), activation='relu', padding='same')(encoded)
x = layers.UpSampling2D((2, 2))(x)
x = layers.Conv2D(8, (3, 3), activation='relu', padding='same')(x)
x = layers.UpSampling2D((2, 2))(x)
x = layers.Conv2D(16, (3, 3), activation='relu')(x)
x = layers.UpSampling2D((2, 2))(x)
decoded = layers.Conv2D(1, (3, 3), activation='sigmoid', padding='same')(x)
autoencoder = keras.Model(input_img, decoded)
autoencoder.compile(optimizer='adam', loss='binary_crossentropy')
为了训练它,我们将使用形状为 `(samples, 3, 28, 28)` 的原始 MNIST 数字,并且我们只会在 0 到 1 之间对像素值进行归一化。
from keras.datasets import mnist
import numpy as np
(x_train, _), (x_test, _) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = np.reshape(x_train, (len(x_train), 28, 28, 1))
x_test = np.reshape(x_test, (len(x_test), 28, 28, 1))
让我们训练这个模型 50 个 epoch。为了演示如何在训练过程中可视化模型的结果,我们将使用TensorFlow 后端和 TensorBoard 回调。
首先,让我们打开一个终端并启动一个 TensorBoard 服务器,它将读取存储在 `/tmp/autoencoder` 的日志。
tensorboard --logdir=/tmp/autoencoder
然后让我们训练我们的模型。在 `callbacks` 列表中,我们传递了一个 `TensorBoard` 回调的实例。在每个 epoch 之后,此回调会将日志写入 `/tmp/autoencoder`,我们的 TensorBoard 服务器可以读取这些日志。
from keras.callbacks import TensorBoard
autoencoder.fit(x_train, x_train,
epochs=50,
batch_size=128,
shuffle=True,
validation_data=(x_test, x_test),
callbacks=[TensorBoard(log_dir='/tmp/autoencoder')])
这使我们能够在 TensorBoard Web 界面(通过导航到 `http://0.0.0.0:6006`)中监控训练
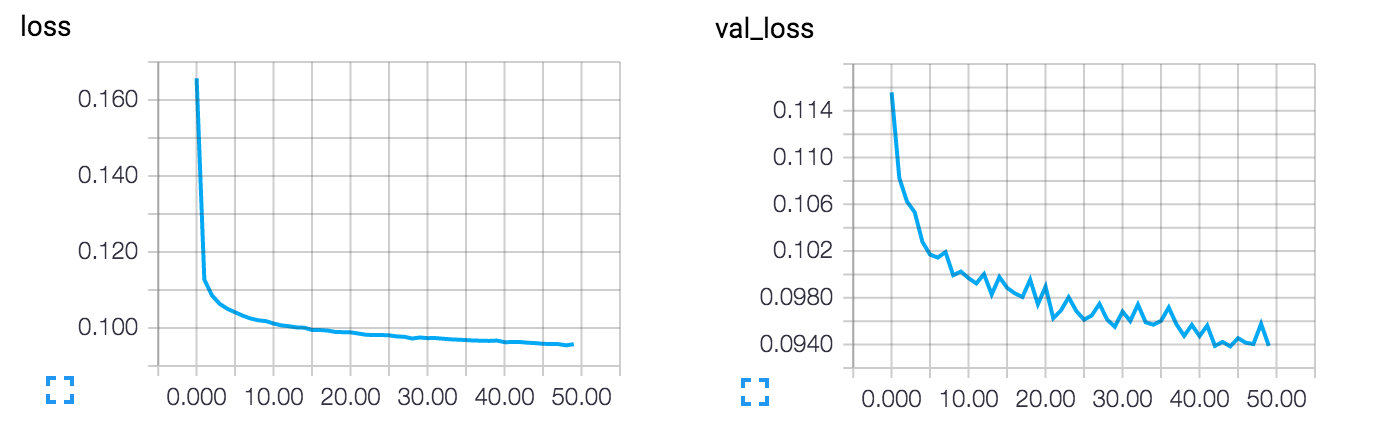
该模型的损失收敛到 0.094,明显优于我们之前的模型(这在很大程度上是由于编码表示的熵容量更高,128 维对之前的 32 维)。让我们来看看重建的数字
decoded_imgs = autoencoder.predict(x_test)
n = 10
plt.figure(figsize=(20, 4))
for i in range(1, n + 1):
# Display original
ax = plt.subplot(2, n, i)
plt.imshow(x_test[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
# Display reconstruction
ax = plt.subplot(2, n, i + n)
plt.imshow(decoded_imgs[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()
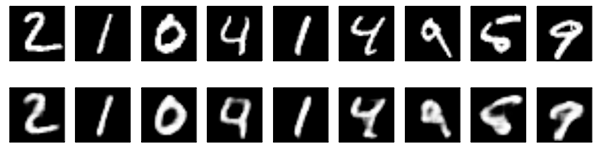
我们还可以看看 128 维的编码表示。这些表示是 8x4x4 的,因此我们将它们 reshape 为 4x32,以便能够将它们显示为灰度图像。
encoder = keras.Model(input_img, encoded)
encoded_imgs = encoder.predict(x_test)
n = 10
plt.figure(figsize=(20, 8))
for i in range(1, n + 1):
ax = plt.subplot(1, n, i)
plt.imshow(encoded_imgs[i].reshape((4, 4 * 8)).T)
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()

图像去噪的应用
让我们将卷积自动编码器用于图像去噪问题。这很简单:我们将训练自动编码器将噪声数字图像映射到干净数字图像。
以下是我们生成合成噪声数字的方法:我们只应用一个高斯噪声矩阵,并将图像剪切在 0 到 1 之间。
from keras.datasets import mnist
import numpy as np
(x_train, _), (x_test, _) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = np.reshape(x_train, (len(x_train), 28, 28, 1))
x_test = np.reshape(x_test, (len(x_test), 28, 28, 1))
noise_factor = 0.5
x_train_noisy = x_train + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=x_train.shape)
x_test_noisy = x_test + noise_factor * np.random.normal(loc=0.0, scale=1.0, size=x_test.shape)
x_train_noisy = np.clip(x_train_noisy, 0., 1.)
x_test_noisy = np.clip(x_test_noisy, 0., 1.)
这是带有噪声的数字图像
n = 10
plt.figure(figsize=(20, 2))
for i in range(1, n + 1):
ax = plt.subplot(1, n, i)
plt.imshow(x_test_noisy[i].reshape(28, 28))
plt.gray()
ax.get_xaxis().set_visible(False)
ax.get_yaxis().set_visible(False)
plt.show()

如果你眯着眼睛看,你仍然可以辨认出来,但很勉强。 我们的自动编码器能否学习恢复原始数字? 让我们来看看。
与之前的卷积自动编码器相比,为了提高重建的质量,我们将使用一个略有不同的模型,每层使用更多的过滤器
input_img = keras.Input(shape=(28, 28, 1))
x = layers.Conv2D(32, (3, 3), activation='relu', padding='same')(input_img)
x = layers.MaxPooling2D((2, 2), padding='same')(x)
x = layers.Conv2D(32, (3, 3), activation='relu', padding='same')(x)
encoded = layers.MaxPooling2D((2, 2), padding='same')(x)
# At this point the representation is (7, 7, 32)
x = layers.Conv2D(32, (3, 3), activation='relu', padding='same')(encoded)
x = layers.UpSampling2D((2, 2))(x)
x = layers.Conv2D(32, (3, 3), activation='relu', padding='same')(x)
x = layers.UpSampling2D((2, 2))(x)
decoded = layers.Conv2D(1, (3, 3), activation='sigmoid', padding='same')(x)
autoencoder = keras.Model(input_img, decoded)
autoencoder.compile(optimizer='adam', loss='binary_crossentropy')
让我们训练 100 个 epochs
autoencoder.fit(x_train_noisy, x_train,
epochs=100,
batch_size=128,
shuffle=True,
validation_data=(x_test_noisy, x_test),
callbacks=[TensorBoard(log_dir='/tmp/tb', histogram_freq=0, write_graph=False)])
现在让我们来看看结果。 上面是输入到网络的噪声数字,下面是由网络重建的数字。

它似乎工作得很好。 如果你将此过程扩展到更大的卷积神经网络,你可以开始构建文档降噪或音频降噪模型。 Kaggle 有一个有趣的数据集可以让你开始。
序列到序列自动编码器
如果你的输入是序列,而不是向量或二维图像,那么你可能希望使用一种可以捕获时间结构的模型作为编码器和解码器,例如 LSTM。 要构建一个基于 LSTM 的自动编码器,首先使用 LSTM 编码器将你的输入序列转换成一个包含整个序列信息的向量,然后重复这个向量 n 次(其中 n 是输出序列中的时间步数),然后运行一个 LSTM 解码器将这个常数序列转换成目标序列。
我们不会在任何特定数据集上演示这个模型。 我们只是在这里放一个代码示例,供读者将来参考!
timesteps = ... # Length of your sequences
input_dim = ...
latent_dim = ...
inputs = keras.Input(shape=(timesteps, input_dim))
encoded = layers.LSTM(latent_dim)(inputs)
decoded = layers.RepeatVector(timesteps)(encoded)
decoded = layers.LSTM(input_dim, return_sequences=True)(decoded)
sequence_autoencoder = keras.Model(inputs, decoded)
encoder = keras.Model(inputs, encoded)
变分自动编码器(VAE)
变分自动编码器是自动编码的一种稍微更新颖和有趣的形式。
什么是变分自动编码器呢?它是一种对学习到的编码表示添加了约束的自动编码器。 更准确地说,它是一个自动编码器,它为其输入数据学习一个 潜在变量模型。 所以,你不是让你的神经网络学习一个任意的函数,而是在学习一个对你的数据进行建模的概率分布的参数。 如果你从这个分布中采样点,你就可以生成新的输入数据样本:VAE 是一个“生成模型”。
变分自动编码器是如何工作的?
首先,编码器网络将输入样本 x 转换成潜在空间中的两个参数,我们将它们记为 z_mean 和 z_log_sigma。 然后,我们通过 z = z_mean + exp(z_log_sigma) * epsilon 从假定生成数据的潜在正态分布中随机抽取类似的点 z,其中 epsilon 是一个随机正态张量。 最后,解码器网络将这些潜在空间点映射回原始输入数据。
模型的参数通过两个损失函数进行训练:一个重建损失,强制解码后的样本与初始输入相匹配(就像在我们之前的自动编码器中一样),以及学习到的潜在分布与先验分布之间的 KL 散度,作为正则化项。 你实际上可以完全去掉后一个项,尽管它确实有助于学习结构良好的潜在空间并减少对训练数据的过拟合。
因为 VAE 是一个更复杂的例子,所以我们已经在 Github 上以 独立脚本 的形式提供了代码。 在这里,我们将逐步回顾模型是如何创建的。
首先,这是我们的编码器网络,将输入映射到我们的潜在分布参数
original_dim = 28 * 28
intermediate_dim = 64
latent_dim = 2
inputs = keras.Input(shape=(original_dim,))
h = layers.Dense(intermediate_dim, activation='relu')(inputs)
z_mean = layers.Dense(latent_dim)(h)
z_log_sigma = layers.Dense(latent_dim)(h)
我们可以使用这些参数从潜在空间中采样新的相似点
from keras import backend as K
def sampling(args):
z_mean, z_log_sigma = args
epsilon = K.random_normal(shape=(K.shape(z_mean)[0], latent_dim),
mean=0., stddev=0.1)
return z_mean + K.exp(z_log_sigma) * epsilon
z = layers.Lambda(sampling)([z_mean, z_log_sigma])
最后,我们可以将这些采样的潜在点映射回重建的输入
# Create encoder
encoder = keras.Model(inputs, [z_mean, z_log_sigma, z], name='encoder')
# Create decoder
latent_inputs = keras.Input(shape=(latent_dim,), name='z_sampling')
x = layers.Dense(intermediate_dim, activation='relu')(latent_inputs)
outputs = layers.Dense(original_dim, activation='sigmoid')(x)
decoder = keras.Model(latent_inputs, outputs, name='decoder')
# instantiate VAE model
outputs = decoder(encoder(inputs)[2])
vae = keras.Model(inputs, outputs, name='vae_mlp')
到目前为止,我们所做的工作允许我们实例化 3 个模型
- 一个将输入映射到重建的端到端自动编码器
- 一个将输入映射到潜在空间的编码器
- 一个可以接收潜在空间上的点并输出相应重建样本的生成器。
我们使用端到端模型训练模型,使用一个自定义损失函数:重建项和 KL 散度正则化项的总和。
reconstruction_loss = keras.losses.binary_crossentropy(inputs, outputs)
reconstruction_loss *= original_dim
kl_loss = 1 + z_log_sigma - K.square(z_mean) - K.exp(z_log_sigma)
kl_loss = K.sum(kl_loss, axis=-1)
kl_loss *= -0.5
vae_loss = K.mean(reconstruction_loss + kl_loss)
vae.add_loss(vae_loss)
vae.compile(optimizer='adam')
我们在 MNIST 数字上训练我们的 VAE
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.astype('float32') / 255.
x_test = x_test.astype('float32') / 255.
x_train = x_train.reshape((len(x_train), np.prod(x_train.shape[1:])))
x_test = x_test.reshape((len(x_test), np.prod(x_test.shape[1:])))
vae.fit(x_train, x_train,
epochs=100,
batch_size=32,
validation_data=(x_test, x_test))
因为我们的潜在空间是二维的,所以在这个时候可以做一些很酷的可视化。 一个是查看潜在二维平面上不同类别的邻域
x_test_encoded = encoder.predict(x_test, batch_size=batch_size)
plt.figure(figsize=(6, 6))
plt.scatter(x_test_encoded[:, 0], x_test_encoded[:, 1], c=y_test)
plt.colorbar()
plt.show()
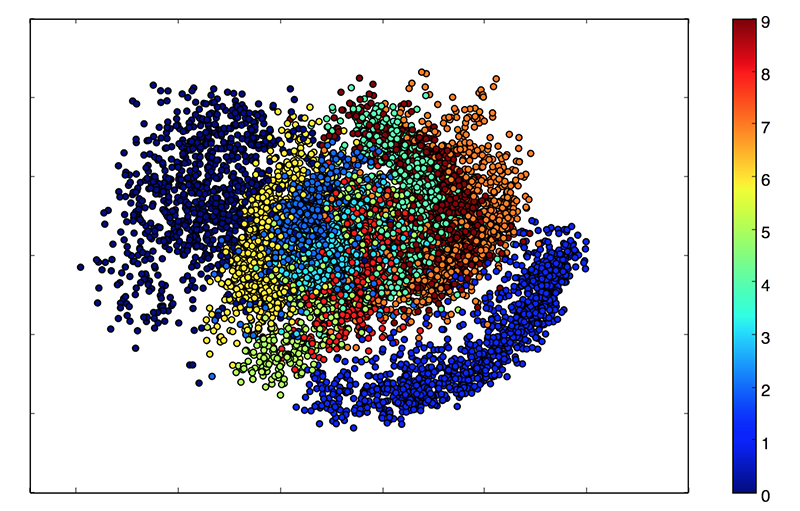
这些彩色集群中的每一个都是一种数字。 接近的集群是结构相似的数字(即在潜在空间中共享信息的数字)。
因为 VAE 是一个生成模型,我们也可以用它来生成新的数字! 在这里,我们将扫描潜在平面,以规则的间隔对潜在点进行采样,并为每个点生成相应的数字。 这就为我们提供了一个“生成”MNIST 数字的潜在流形的可视化。
# Display a 2D manifold of the digits
n = 15 # figure with 15x15 digits
digit_size = 28
figure = np.zeros((digit_size * n, digit_size * n))
# We will sample n points within [-15, 15] standard deviations
grid_x = np.linspace(-15, 15, n)
grid_y = np.linspace(-15, 15, n)
for i, yi in enumerate(grid_x):
for j, xi in enumerate(grid_y):
z_sample = np.array([[xi, yi]])
x_decoded = decoder.predict(z_sample)
digit = x_decoded[0].reshape(digit_size, digit_size)
figure[i * digit_size: (i + 1) * digit_size,
j * digit_size: (j + 1) * digit_size] = digit
plt.figure(figsize=(10, 10))
plt.imshow(figure)
plt.show()

就是这样! 如果你对这篇文章(或未来的文章)中要涵盖的更多主题有任何建议,你可以在 Twitter 上联系我 @fchollet。
参考文献
[2] 批量归一化:通过减少内部协变量偏移加速深度网络训练。
[3] 用于图像识别的深度残差学习
[4] 自动编码变分贝叶斯